(~KR2)
Students from Oakwood High School (Morgan Hill, CA) noticing cool examples of geometric objects and concepts in the world around them.
Wednesday, April 30, 2014
Home Decorating
(~KR2)
Friday, April 25, 2014
Fractals in Fruit
We bought a pineapple for dinner yesterday and I noticed the individual small fruits that made up the entire pineapple were fractals. A fractal is a mathematical set that typically displays self-similar patterns. Fractals can be exactly the same each time they are repeated, or like in my picture, almost the same each time. These fractals aligned just so that I could see a part of the Fibonacci Sequence. The Fibonacci Sequence is a series of numbers where each number is the sum of the two previous numbers. For example, the 5 yellow fractals and the 8 green fractals make up the 13 blue fractals in my picture. I thought this was fascinating because I never really paid attention to the way fractals make up entire objects and how the Fibonacci Sequence is common in nature. (~MG1)
Bent Shower Rod
This past week I went to Monterrey with my mom for a little vacation. We stayed in a small hotel and while there I noticed the bent shape of the shower rod. I immediately thought of geometry.
After drawing in a straight bar and calculating the area of the triangle formed versus the increased area with a bent shower rod:
I concluded that the bent rod greatly increases the space within the shower.
37.31-21.63= 15.68 cm-squared more space.
This is probably one of the simplest yet one of the most useful inventions for everyday life. (~LU2)
After drawing in a straight bar and calculating the area of the triangle formed versus the increased area with a bent shower rod:
I concluded that the bent rod greatly increases the space within the shower.
37.31-21.63= 15.68 cm-squared more space.
This is probably one of the simplest yet one of the most useful inventions for everyday life. (~LU2)
Sunday, April 20, 2014
Weave of a Rattan Chair
I saw this chair in my house and I noticed that the backrest is a tessellation.
After zooming into the weave pattern I realized that the pattern was made up of triangles and circles. Ideally, all of the triangles should have the same side lengths and angle measures, but this is not true because the width of each rattan strip is not the same. (~LSU2)
Tuesday, April 15, 2014
The Golden Ratio
If you could calculate the ratio between the each of the sections to the next, you would find that the ratio is the same as the Golden Ratio. (~CB1)
Wednesday, April 2, 2014
Congruent Circles
I remembered how in class we talked about how six congruent circles could perfectly encompass another congruent circle in the middle and I wanted to see it my self. Here it is with the measurements to prove they are congruent. (DF5)
Angles and Arcs in Clocks
In this picture angle EJF equals 135.15 and is congruent to its arc EF which equals 135.19. This is because a central angle inscribed in a circle is congruent to its arc.
[Note: The numbers are slightly off though because the angle is not exactly in the center of the clock. This makes the numbers not perfectly equal but if the angle was in the center the angle and the arc would be congruent.]
(~AD1)
Proving Theorem 9-5 with a Car Tire
As theorem 9-5 states, "a diameter that is perpendicular to a chord bisects the chord and its arc." I decided to use a picture of my car tire to show the proof of this theorem.
Geometrii
When I walked by my TV, I noticed this Wii remote wheel. I then wanted to test out the theorem that states that the product of one secant segment and its external segment equals the product of the other secant segment and its external segment. I soon found that the theorem holds true, and the products of the lengths were equal. ~(DM2)
Common Tangents
After finding these materials in my room, I noticed that I was staring at a circles that had both internal and external common tangents. You could see both of the ways that made this true. The top picture shows that the two circles could share an internal common tangent, and the second picture below shows the circles with common external tangents. (~MC2)
Tuesday, April 1, 2014
The Truth About Circles
This illustration demonstrates that when you multiply the whole secant by the section outside of the circle, its product is congruent to the other secant multiplied by the other section outside the circle. (~MM2)
Arcs and Central Angles
This picture is of a CD disk in its cover. This picture shows two different ideas. One idea is a quadrilateral circumscribed about a circle. The cover fits around the disk like a quadrilateral circumscribed about a circle. The second idea is arcs and central angles. Point A is the center point here. Arc BC is approximately 37 degrees. The central angle CAB is also 37 degrees.
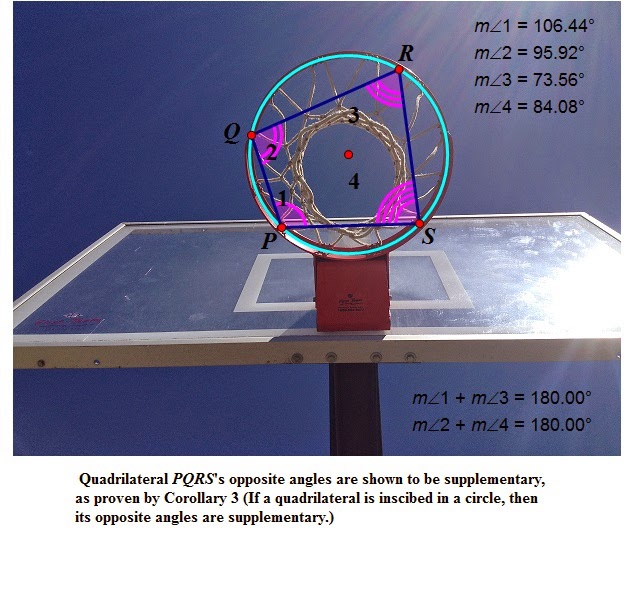
Inscribed Angles and Three Corollaries
Corollary 1: If two inscribed angles intercept the same arc, then the angles are congruent.
Corollary 2: An angle inscribed in a semicircle is a right angle.
And finally,
Corollary 3: If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary.
(~RO5)
Concentric Circles
While going through my bookshelf I noticed that one of my books had an interesting design on it. These circles that are known as Concentric Circles. They all lie in the same plane and have the same center. Also the lines going through the circles are called secants. (~AV5)
The Circular Olive
"If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary."
This corollary is clearly proven through the addition of the opposite angles of the quadrilateral I drew within this circle on GSP. (~AI5)
Soda Pong with Tangents
While I was setting up a clean game of Soda Pong, I took a close look at the formation of the cups. I then saw that the brims of the cups were externally tangent circles. The cups touch at a point of tangency. The radii of the cups are the same and they fit. This makes it able for exactly six cups to fit around one center cup. It was a great game that also allowed me to find my next Geometry Hunters post.(~KM5)
Rims
Here is something cool I noticed about the rims on this car.
This car's rims form a circle, which also have smaller circles inside of them.
As you can see, there is one big circle containing five smaller circles. These circles all appear to be similar. I drew radii for all the circles aiming towards the center of the rim, and they appeared to form a pentagon.
I thought it was really cool that this car's rims contained many circles which could form other geometric objects. - (DM5)
Happiest Geometry on Earth
This is an old picture that I took while I was at Disneyland. It is the Mickey Mouse Ferris Wheel. I noticed that it is a perfect example of radii in a circle. Each line goes from the outside to the middle, which is the Mickey Mouse's head. (~CD1)
Cymbals with Tangents, Chords, & Secants
Over the weekend, I acquired two new cymbals and I thought I'd make use of them, other than for music. In this first illustration, I proved that the result of multiplying two pieces of individual chords should be equal. I simply multiplied AE x EC (the labels you can't see very well, sorry,) the first chord, and then BE x ED, the second chord, and they both came out to be 34.36 cm sq.
In this second picture, I demonstrated that the tangent of a circle multiplied by itself, is equal to the outside piece of a secant multiplied by the entire length of the secant. I squared AB which resulted in 200.77 cm sq, and multiplied AC x AD, which resulted in 200.77 cm sq as well. This proves that the tangent squared does equal the secant length times the outer piece. (~JG2)
Angles on a Clock
When I was looking at my clock I noticed that not only could I find the angles made by radii of the triangles but also secants using the theorems in chapter 9. By theorem 9-4 I determined that the measure of angle BCD was equal to the measure of arc BD. From that I was able to use theorem 9-7 to prove the measure of angle BAD is equal to half of arc BD. Therefore the measure of angle BAD is equal to half of the measure of angle BCD. (~AL1)
GIRL
At my local swimming pool, I found a women's bathroom sign with the shape of a perfect circle and was wondering if I could prove any geometric theorems with it.
On Geometer's Sketchpad, I drew a tangent of the circle and a secant to the circle. I planned to prove theorem 9-10 which states that two secants, two tangents, or a secant and a tangent follow the same equation. The angle that is formed by the intersecting lines would be equivalent to 1/2 the quantity of the major arch created minus the minor arch created.
Through GSP, I have proven that no matter what size or angle, the equation works every time.
(~WM5)
Books
This is a picture of a bunch of different symbols from books put together (Percy Jackson, Harry Potter, The Mortal Instruments, The Hunger Games, Divergent).
In this picture, there are three circles. The center one is externally tangent to both of the circles on either side of it. The vertical line in the middle of the picture is also the diameter of the center circle.
This image also has two lines that are externally tangent to the center circle (lines j and k). The right angles formed by the radii to the tangency point prove that the lines are tangent.
~CS1
Congruent Tangents
GC2
Tangents to a circle from a point are congruent. (Corollary)
 I brought my camera to an ice cream parlor last week in hopes of finding an example of the corollary stated above. According to this corollary, tangents to a circle from a point are congruent. I found my ice cream cone to be a great example of this. In the picture, segments AB and AC are both tangent to the circle (scoop) at points B and C. This should assure that tangent AB is congruent to tangent AC, which was further proven when I measured the segments using GSP.
I brought my camera to an ice cream parlor last week in hopes of finding an example of the corollary stated above. According to this corollary, tangents to a circle from a point are congruent. I found my ice cream cone to be a great example of this. In the picture, segments AB and AC are both tangent to the circle (scoop) at points B and C. This should assure that tangent AB is congruent to tangent AC, which was further proven when I measured the segments using GSP.
Subscribe to:
Posts (Atom)