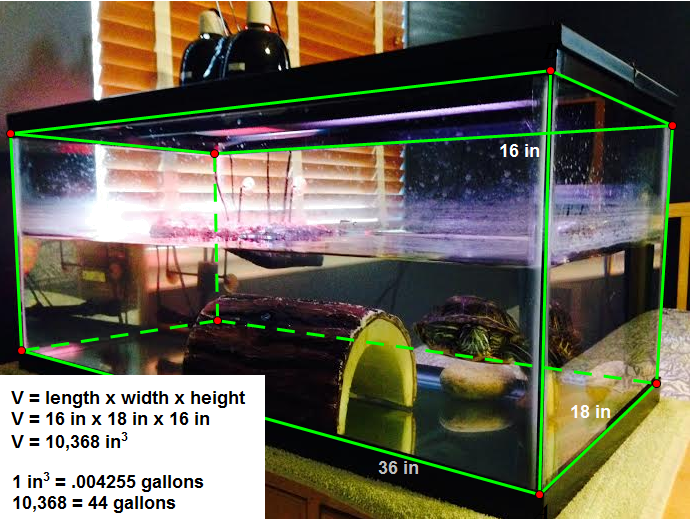
Turtle Tank

Since we have been learning about volume, I wanted to put our learning to work. My brother said that he wasn't sure how many gallons his turtle tank could hold, so I measured all the lengths and used the formula. It turns out that the volume of this tank is about 44 US gallons. Note, if my brother ever wanted to figure out how many gallons he has currently in the tank, we could just use the same formula, find the volume, and subtract that from the original 44. (TF~2)

Pyramid

This is something I made a few years ago for a school project. It is in the shape of a regular square pyramid.

With the given dimensions, the pyramid would have a volume of about 572.33cm³ and a lateral area of 344.2008cm³. (~CS1)

Cylinders

-SV(1)

Area of the Side of a Goal

I noticed that the side of the soccer goal was almost a trapezoid and I decided to use it to find area.

To find the area of the side I extended the lines to make a trapezoid than subtracted the area of the small triangle.

 

Using GSP measurements the area of the shape made by the side of the goal is 45.2395cm^2.
(NW5)

Tennis Balls

 

I was on my way to hit the courts when I came across a tennis ball along with a can of three tennis balls. I remembered a math problem with a sphere and a cylinder and comparing their volumes. So I decided to insert the image into gsp and use geometry in my real life. I used the formula for the volume of a cylinder and the formula for the volume of a sphere and found that the volume of the ball was around 3 cm cubed and the volume of the cylinder was around 13 cm cubed. Meaning that the space in between the balls would account for about one extra ball. (~WM5)

The Presence of the Golden Ratio

In infamous Golden Ratio has been seen in everything from art, to nature, to even the proportions of human beings. It has continued to astound artists, scientist, and mathematicians for centuries.

Simply put, the Golden Ratio is a special number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part.

The unique properties of the Golden Rectangle provides another example. The Golden rectangle is one in which the ratio of the sides a/b is equal to the golden mean (also referred to by the Greeks as phi), can result in a repeating process that can be repeated into infinity — and also takes on the form of a spiral. It is the most common form of the Golden Ratio in nature.

Countless examples around us are in the proportion of the Golden Ratio.

Some of the most interesting and unique examples of the Golden Ratio which cause us to think that things being in the Golden Ratio are not merely a coincidence are shown below:

The Nautilus Shell:

The Nautilus Shell follows the "logarithmic spiral", also known as the result of the proportion of the Golden Rectangle. 

Galaxies:

The Milky Way galaxy contains several "spiral arms", each of them a logarithmic spiral and containing the proportions of the Golden Ratio.

Memorable Geometry

On our 8th grade East Coast trip, we visited the Washington Monument.  I was able to take a lot of great photos of it and was also able to find some hidden geometry.  The part of the monument outlined in red is a right rectangular prism.  It's a bit hard to see, but imagine looking down on it from the sky.  This prism makes up the base of the monument and it has four lateral faces.  It also has four lateral edges and two bases.  Theorem 12-1 states that the lateral area of a right prism equals the perimeter of a base times the height of the prism, or L.A. = ph.  Theorem 12-2 states that the volume of a right prism equals the area of a base times the height of the prism or V = Bh.  Finally, the surface area of the prism equals the lateral area plus 2 times the area of the base.

On the very top of the monument rests a pyramid.  It is outlined in blue in the picture.  It also has four lateral faces and lateral edges.  The pyramid's vertex acts as the top of the monument and it shares one of the prism's 2 bases.  Theorem 12-3 states that the lateral area of a regular pyramid equals half of the perimeter of the base times the slant height or L.A. = 1/2pl.  Theorem 12-4 states that the volume of a pyramid equals one third the area of the base times the height of the pyramid or V = 1/3Bh.  Lastly, the surface area of the pyramid equals the lateral area plus the area of the base.  So, not only does the Washington Monument represent one of our greatest founding fathers, but it represents the beauty of geometry. ~MG1  

    

Scale Factor

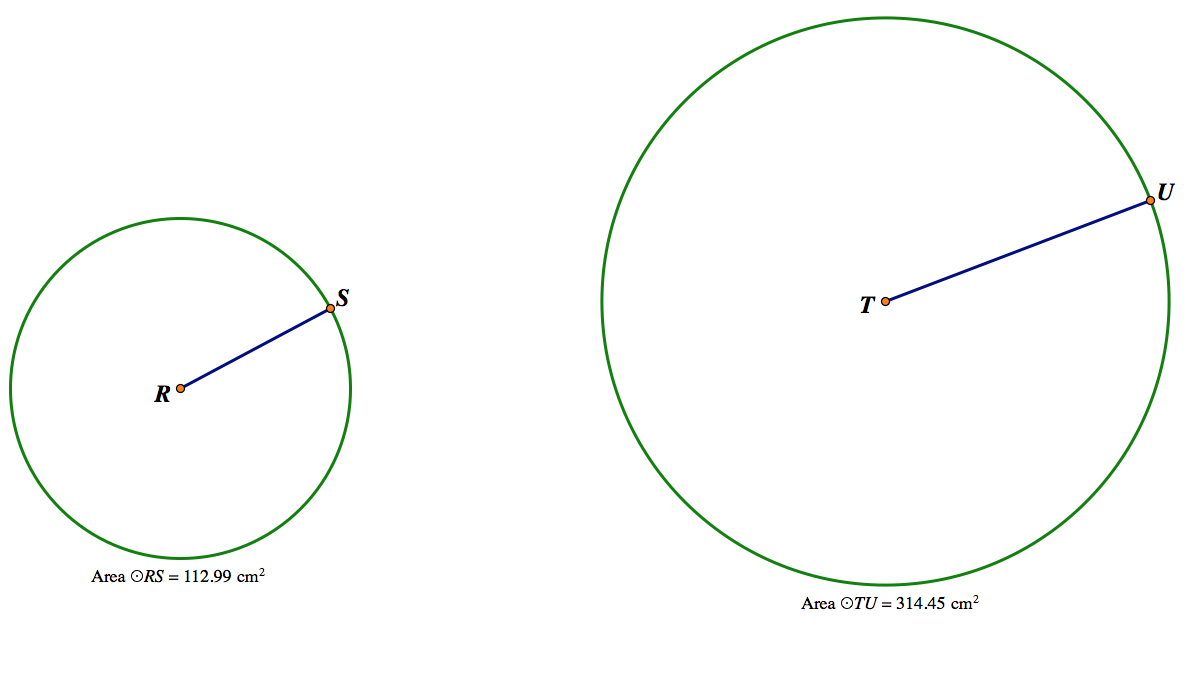
Here, I will be using similar polygons (circles) and showing their scale factors for units and units squared. Here are two ordinary circles, one with radius of 6, and one with radius of 10. Their scale factor is 6 divided by 10, and that simplified is 3:5.

Now when we find the circumferences of the two circles, their ratio should be the same as the ratio of the radii.

The circumferences of the two circles are 37.68 and 62.86. When we divide 37.68 by 62.86, we get .60, which is equal to 3 divided by 5. 

The areas of the circles should be in the scale factor of k squared, in other words, 3 squared / 5 squared.  The scale factor for the areas of the circles should be 9:25.

The area for the first circle is 112.99 square cm, and the area for the second circle is 314.45 square cm. If we divide 112.99 by 314.45, we get .36, which is the same as 9/25. This demonstrates that if we have any two similar polygons, any length measured in units is in the scale factor k, and anything measured in units squared is in the scale factor k squared. (~DM5)

Proof of Parallels

My brother recently had surgery and will be restricted to a wheelchair for the next six weeks. Because of this, we need wheelchair ramps on our steps so he has access to the house. The wheels on a wheelchair are parallel, so the ramps must be parallel or the wheelchair cannot successfully scale the ramps. I can prove that the wheels are parallel, and that the ramps are close enough to parallel to allow the wheelchair to travel up and down them.

Because of the angle at which the pictures were taken, the ramps appear slightly crooked, but I can assure you that they are not. If you zoom out, you can see this.

(~CB1)

Measuring Lateral Area and Volume of a Cone

After finding a three dimensional cone in the art room, I decided to put it to use to find its circumference and area, as well as use Theorem 12-7 and 12-8 to find its lateral area and volume.

First, I began by measuring the cone's height (h) and slant height (l).

Next, I measured the radius, and used that to calculate both the circumference of the base and the area.

After collecting all the needed information, I put it to use to calculate lateral area using Theorem 12-7, and volume using Theorem 12-8.

Theorem 12-7: The lateral area of a cone equals half the circumference of the base times the slant height.

Theorem 12-8: The volume of a cone equals one third the area of the base times the height of the cone.

(~RO5)

Tessellations in Boston

While we were in Boston for our D.C. trip, I noticed a sidewalk that contained tessellations. The shapes fit in perfectly with no gaps or spaces. The pattern would be able to continue indefinitely. The basic definition of a tessellation is a random shape repeated over and over covering a plane with out any gaps or overlaps. Another word is tiling.

   

















Some further research shows that there are two main types of tessellations: regular and semi-regular.

Regular tessellations are patterns made by repeating a regular polygon. In that case there are only three types: squares, triangles and hexagons. For regular tessellations, the pattern is always the same at the vertex.

A semi-regular tessellation consisted of two or more regular polygons. As with the regular tessellations, the patterns must be the same at each vertex. (~IR1)

Surface Area of the Pentagon

When I was in Washington D.C. last week I noticed that the pentagon was just a regular pentagonal prism. With this I searched online to figure out the height and side length of the Pentagon. From these dimensions I was able to figure out the Lateral Area and the Surface Area of the Pentagon. (~AL1)

Circumference, Area, and Pie

After taking a picture of this fruit pie (because everyone takes a picture of their food before they eat it these days) I noticed that this pie was a perfect example of a circle, and using some simple formulas, I could find its circumference and area.

After measuring a radii of the circle, I was able to calculate the area and circumference using the formulas shown above. 

But, why stop there? It also became apparent that I could inscribe a polygon inside the circle, and calculate the area of that as well. In this case, I used a trapezoid.

As shown above, I was able to calculate the area of this trapezoid using Theorem 11-5.

It's seems that everything, even a fruit pie, has some relation to math, and more specifically: geometry. 

-RO5

Hexagonal Prism

This is a hexagonal prism that I bought at a souvenir shops in Washington D.C. It is really cool and shows a bunch of famous monuments and buildings in D.C. which are on each side of the prism. The Washington Monument is in the middle. I saw this and remembered calculating lateral area, surface area, and volume, with prisms just like this one.

(~SV1)

Geometric Structures from the East Coast Trip

This is one of the watch towers from the Berlin Wall. I took this picture at the Newseum in Washington, D.C. The watch towers were shaped like right square prisms.

The Holocaust memorial in Boston was also shaped like a prism.

More prisms on the skyline picture of New York from the ferry to the Statue of Liberty. 

All of the skyscrapers are either square right prisms or rectangular right prisms.

(~CS1)

Cubic Net

Here we have a the net of a cube. A net is defined as “any set of polygons joined edge to edge that, when folded along the edges between adjoining polygons so that the outer edges touch, form a polyhedron” (Wiktionary). It is clear that each side of the square is a length of 5 units. It is also much easier to see that a cube has six faces, and therefore easier to calculate the surface area of the cube:
5 x 2 x 6 = 150 square units.

Here is the folding process.

Here is the finished product: the cube. It is easier to see how to calculate the volume of the cube now, as it is 3-Dimensional now as opposed to 2-Dimensional. 53 = 125 cubic units.

Square Area of the Cube: 150 square units.
Volume of the Cube: 125 cubic units.

~JC1

Geometry in an Old Sailing Ship

This picture shows an example of perpendicular lines in the ship's sail and mast. There are also examples of an isosceles triangle in the ropes on top. In the middle, there is a crows nest that shows an example of a circle, with the mast going through its center. (~CD1)

Shadows

The shadow of the fence shows intersecting and parallel lines. It also shows congruent polygons. There are isosceles triangles at the top of the fence that also seem to be congruent. (-CD1)

Parallelogram in Railing

I noticed that the railing next to some stairs formed a parallelogram.

This parallelogram can be proved as a parallelogram since opposite angles are congruent.

If you draw a line from angle A to angle C, you can show theorem 5-11 which states that the segment that joins the midpoints of two sides of a triangle is 1. parallel to the third side and 2. half as long as the third side.

In the diagram this theorem is proved because 1. EF is parallel to BA which is shown by corresponding angles being congruent and 2. EF=15.60cm which is half as long as the 31.20cm length of BA.

Finally,  the area of a parallelogram is bh.  To find the height I drew an altitude from angle C down and used  sin of angle B

(∼NW5)

Decorative Segment

 I was walking through my living room when suddenly I saw a Chinese style decorative plate and it happened to remind me of our latest chapter of geometry. I decided to show how to find the area of a segment.

As you can see, I went in GSP and drew what it would look like. I drew two radii, which happened to form a 120 degree angle. Area is pi radius squared, so I divided it by three because the circle was cut into three equal sections. Then I calculated the area of the triangle with the Pythagorean Theorem and subtracted the whole section from the area of the triangle. (~WM5)

Tangent Coins

Here are two ordinary coins, a quarter and a nickel. I am going to draw an external tangent from the quarter to the dime. I will be showing how drawing a line from the center of one of the coins (or circles in this case) to the point of tangency will form a right angle.

It is clear that the angle drawn from the center of the dime to its point of tangency (on the tangent shared with the quarter) is roughly 90 degrees, thus proving that any line drawn from the center to a point of tangency creates a 90 degree angle.

It is also seen here that the line from the point of tangency to the center creates a 90 degree angle.

(~DM5)

Hamster Wheel

I was feeding my hamster and noticed the wheel that she runs on. On the wheel are two steel segments that are running through the circle. These segments are both congruent and are both the diameter of the wheel. Since the chords of the circle (the diameter) are congruent this displays Theorem 9-4, which is that congruent chords have congruent arcs. Both the arcs share the same central angle which also prove that the arcs would be congruent. (~AV5)

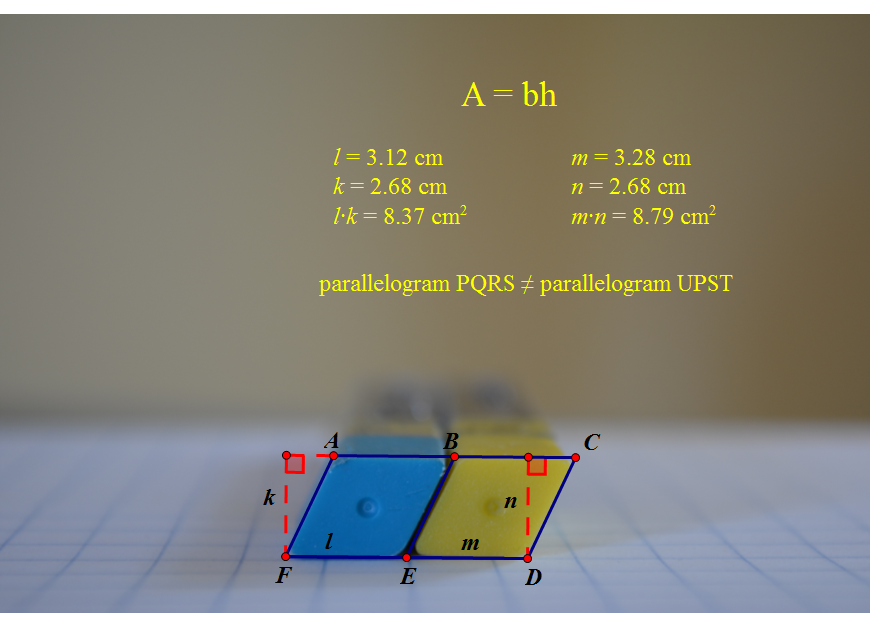
Congruent Parallelograms?

Although you may not be able to tell by the picture, these blue and yellow parallelograms are the tops of two led containers for my mechanical pencil. I traced them with help from the construct>parallel line, construct>perpendicular line, and construct>midpoint tools in The Geometer's Sketchpad.
I drew two altitudes (k and n) in order to find the height of each parallelogram. Then, I multiplied each height by its corresponding base and, to my surprise, found these parallelograms to not have equal areas, and therefore not be congruent.
The total area of parallelogram ACDF is 17.16 square centimeters.
(~GC2)

Baskets and Circles

I saw this basket that was holding oranges in my house and realized that it had an interesting design on it. The diameter is splitting the circle in half creating two congruent arcs. The other two chords in the circle share the same central angle. This means that the arcs would be congruent based off theorem 9-3, which is that if arcs share central angles then they are congruent. the chords would also be congruent because congruent arcs have congruent chords. (~KM5)